riskprog
riskprog solves risk minimization problems with linear constraints on variables.
Mathematical Problem Statement
Finds a minimum for a problem specified by
![]()
subject to
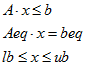
where
A, Aeq are matrices;
d, x are column vectors;
b, beq, lb, ub are column vectors or scalars;
risk function is a linear combination of PSG risk functions, PSG deterministic functions, or a PSG utility functions (see List of PSG functions for riskprog).
xout = riskprog (risk, w, H, c, p, d, A, b)
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq)
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq, lb, ub)
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq, lb, ub, x0)
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq, lb, ub, x0, options)
[xout, fval] = riskprog (…)
[xout, fval, exitflag] = riskprog (…)
[xout, fval, exitflag, output] = riskprog (…)
Remarks
Omitted parameters should be substituted by square brackets “[]”.
xout = riskprog (risk, w, H, c, p, d, A, b) returns a vector xout minimizing objective ![]() subject to
subject to ![]() . Risk function is specified by risk, w, H, c, and p.
. Risk function is specified by risk, w, H, c, and p.
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq) solves the problem satisfying additionally the equality constraints ![]() .
.
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq, lb, ub) solves the problem with lower and upper bounds on the decision point x, such that the decision point is in the range ![]() .
.
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq, lb, ub, x0) sets the initial point x0.
xout = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq, lb, ub, x0, options) minimizes with the optimization options specified in the structure options.
[xout, fval] = riskprog (…) returns the value of the objective function at x: ![]() . Risk function is specified by risk, w, H, c, and p.
. Risk function is specified by risk, w, H, c, and p.
[xout, fval, status] = riskprog (…) returns the problem status ={ optimal | feasible | unbounded | infeasible } describing the status of solved optimization problem.
[xout, fval, status, output] = riskprog (…) returns the structure output containing resulting information about the optimization with riskprog .
risk |
string with description of PSG function (objective include only one PSG function) or cell array with coefficients (real) and PSG functions (string) of the form: {coefficient 1, 'function 1', ... , coefficient K, 'function K'}. See, List of PSG functions for riskprog; |
w |
parameter (real) of the PSG function (for one PSG function in objective) or cell array of parameters (for linear combination of PSG functions; order of parameters are the same as the order of functions in risk). If parameter is not present, then substitute parameter by square brackets “[]” ); |
H |
matrix for one PSG function in objective risk or cell array of matrices for linear combination of PSG functions risk (order of matrix are the same as the order of functions in risk); |
c |
vector of benchmark for one PSG function in objective risk or cell array of vectors of benchmarks for linear combination of PSG functions risk (order of vectors are the same as the order of functions in risk). If the benchmark is not used, then substitute it by square brackets “[]”; |
p |
vector of probabilities for one PSG function in objective risk or cell array of vectors of probabilities for linear combination of PSG functions risk (order of vectors are the same as the order of functions in risk). If all probabilities are equal, you can substitute p by square brackets “[]”); |
d |
column vectors for linear component of objective; |
A |
matrix for linear inequality constraint; |
b |
vector or scalars for linear inequality constraint; |
Aeq |
matrix for linear equality constraint; |
beq |
vector for linear equality constraint; |
lb |
vector of lower bounds for x; |
ub |
vector of upper bounds for x; |
x0 |
initial point for x (see Initial Point); |
options |
structure that contains optimization options (see Options). |
Strucure output contains information about the optimization. The fields of the structure are:
xout |
optimal point; |
fval |
optimal value of objective function |
frval |
optimal values of PSG functions defined in objective; |
fdval |
optimal values of linear component of objective; |
fAval |
optimal values of left hand sides of linear inequality constraints; |
rAval |
residual of linear inequality constraints; |
fAeqval |
optimal values of left hand sides of linear equality constraints; |
rAeqval |
residual of linear equality constraints; |
data_loading_time |
data loading time; |
preprocessing_time |
preprocessing time; |
solving_time |
solving time. |
Structure options contains optimization options used by riskprog. The fields of the structure are:
Solver |
choose optimization PSG solvers from a list: VAN, CAR, BULDOZER, TANK (for more details see Optimization Solvers); |
Precision |
number of digits that solver tries to obtain in objective and constraints; |
Time_Limit |
time in seconds restricting the duration of the optimization process; |
Stages |
number of stages of the optimization process (this parameter should be specified for VaR, Probability, and Cardinality groups of functions). |
Linearization |
controls internal representation of risk function, which can speed up the optimization process (used with CAR and TANK solvers). 'On' or 'Off' (default) (see Linearizing); |
Path_to_Export_to_Text |
string with path to the folder for storing problem in General (Text) Format of PSG). If Path_to_Export_to_Text=‘’ (default) than the problem is not exported in General (Text) Format of PSG; |
Path_to_Export_to_MAT |
string with path to the folder for storing problem as mat-file. If Path_to_Export_to_MAT=‘’ (default) than the problem is not exported as mat-file. This option is intended for converting the problem to the PSG MATLAB Data Structure; |
Display |
key specifying if messages that may appear when you run this subroutine should be suppressed (Display = 'Off') or not (by the default: Display ='On') (see PSG Messages); |
Warnings |
key specifying if warnings that may appear when you run this subroutine should be suppressed (Warnings = 'On') or not (by the default: Warnings ='Off'); (see PSG Messages) |
Types |
specifies the variables types of a problem. If Types is defined as column-vector, it should include as many components as number of variables Problem includes. The components of column-vector can possess the values "0" - for variables of type real, or 1- for variables of type boolean, or 2 - for variables of type integer. If Types is defined as one number (0, or 1, or 2) than all variables types real, or boolean, or integer respectively. |
In this example we use the problem description similar to the defined in the section Quick Start with PSG MATLAB problem of CVaR minimization (see PSG Function cvar_risk). The constraint for average returns is dropped.
Find ![]() minimizing
minimizing
![]()
subject to
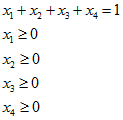
Run the following example from the folder./Aorda/PSG/MATLAB/Examples/Problems/Example_CVaR_riskprog.m or type the next PSG problem in MATLAB:
Define input data:
H=[1,4,8,3; 7,5,4,6; 2,8,1,0; 0,3,4,9];
c=[0.2; 0.11; 0.6; 0.1];
Aeq=[1, 1, 1, 1];
beq=1;
lb=[0; 0; 0; 0];
p=[];
Next, run the subroutine (see riskconstrprog function):
[xout, fval, status, output] = riskprog('cvar_risk', 0.95, H, c, [], [], [], [],Aeq, beq, lb);
You get the following output:
Optimal point:
xout =
0
0.5959
0.1929
0.2112
Objective value on the optimal point:
fval =
-4.3602
Status of the solved optimization problem:
status =
optimal
Full report for solution of the optimization problem:
output =
xout: [4x1 double]
fval: -4.3602
frval: -4.3602
fdval: []
fAval: []
rAval: []
fAeqval: 1.0000
rAeqval: 4.4409e-016
data_loading_time: 0
preprocessing_time: 0
solving_time: 0
riskparam, riskconstrprog, riskcontparam, riskratioprog
List of PSG functions for riskprog
Subroutine riskprog works only with PSG functions described in this section.
Remarks
| • | Exponential Utility, Logarithmic Utility, Power Utility, Logarithms Sum, and Logarithms Exponents Sum functions are included in the objective with the negative coefficient -1 by default. However, you should not set any coefficient for these functions, riskprog sets it automatically. If risk function is a PSG risk, cardinality, or nonlinear function (except for Logarithms Sum and Logarithms Exponents Sum functions), then riskprog minimizes the objective |
| • | linear, pr_dev, pr_dev_g, pr_pen, and pr_pen_g PSG functions should NOT be combined with the vector d (substitute d by square brackets “[]” ). |
| • | Relative Entropy function (entropyr) can have up to 100,000,000 decision variables if Linearization='On' option is specified. This option may dramatically speedup calculations. In this case BULDOZER solver is recommended. |
The following PSG functions can be minimized by riskprog.
Full Name |
Brief Name |
Short Description |
|---|---|---|
avg |
Average Loss obtained by averaging Linear Loss scenarios, i.e., it is a linear function with coefficients obtained by averaging coefficients of Linear Loss scenarios. |
|
avg_g |
Average Gain obtained by averaging -(Linear Loss ) scenarios, i.e., it is a linear function with coefficients obtained by averaging coefficients of -(Linear Loss) scenarios. |
|
buyin |
For a finite dimension vector, buyin equals the number components satisfying two conditions: 1) absolute value of a component exceeds threshold_1; 2) if a component is positive, then its absolute value is below threshold_2, otherwise its absolute value is below threshold_3 |
|
buyin_neg |
Number of components of -(vector) exceeding threshold_1 and below threshold_2 |
|
buyin_pos |
Number of components of a vector exceeding threshold_1 and below threshold_2 |
|
cardn |
Number of absolute values of components of a vector exceeding some threshold |
|
cardn_neg |
Number of components of -(vector) exceeding some threshold |
|
cardn_pos |
Number of components of a vector exceeding some threshold |
|
cdar_dev |
For every time moment, j=1,...J , portfolio drawdown = d(j) = maxn ((uncompounded cumulative portfolio return at time moment n ) - (uncompounded cumulative portfolio return at time moment j )). CDaR = CVaR Component Positive of vector (d(1), ..., d(J)) = average of the largest (1-α)% components of the vector (d(1), ..., d(J)), where 0≤α≤1 . |
|
cdar_dev_g |
For every time moment, j=1,...J , portfolio -drawdown = -d(j) = maxn (-(uncompounded cumulative portfolio return at time moment n ) + (uncompounded cumulative portfolio return at time moment j )). CDaR for Gain = CVaR Component Positive of vector (-d(1), ...,- d(J)) = average of the largest (1-α)% components of the vector (-d(1), ..., -d(J)), where 0≤α≤1 . |
|
cvar_comp_abs |
Scaled CVaR Norm = Average of the largest (1-α)% of absolute values of components of a vector, where 0≤α≤1 |
|
cvar_comp_neg |
Average of the largest (1-α)% of components of a -( vector), where 0≤α≤1 |
|
cvar_comp_pos |
Average of the largest (1-α)% of components of a vector, where 0≤α≤1 |
|
cvar_dev |
Conditional Value-at-Risk for (Linear Loss) - (Average over Linear Loss scenarios) , i.e., the average of largest (1-α)% of (Linear Loss) - (Average over Linear Loss scenarios) scenarios. |
|
cvar_dev_g |
Conditional Value-at-Risk for -(Linear Loss ) + (Average over scenarios Linear Loss) , i.e., the average of largest (1-α)% of - (Linear Loss) + (Average over scenarios Linear Loss) scenarios. |
|
cvar_risk |
Conditional Value-at-Risk for Linear Loss scenarios (also called Expected Shortfall and Tail VaR), i.e., the average of largest (1-α)% of Losses. |
|
cvar_risk_g |
Conditional Value-at-Risk for -(Linear Loss ) scenarios (also called Expected Shortfall and Tail VaR), i.e., the average of largest (1-α)% of -(Losses). |
|
drawdown_dev_avg |
For every time moment, j=1,...J , portfolio drawdown = d(j) = maxn ((uncompounded cumulative portfolio return at time moment n ) - (uncompounded cumulative portfolio return at time moment j )). Drawdown Deviation = average of components of the vector (d(1), ..., d(J)) . |
|
drawdown_dev_avg_g |
For every time moment, j=1,...J , portfolio -(drawdown) = -d(j) = maxn (-(uncompounded cumulative portfolio return at time moment n ) + (uncompounded cumulative portfolio return at time moment j )). Drawdown Average for Gain = average of components of the vector (-d(1), ...,- d(J)). |
|
drawdown_dev_max |
For every time moment, j=1,...J , portfolio drawdown = d(j) = maxn ((uncompounded cumulative portfolio return at time moment n ) - (uncompounded cumulative portfolio return at time moment j )). Drawdown Maximum = Maximum Component Positive of vector (d(1), ..., d(J)) = largest component of the vector (d(1), ..., d(J)). |
|
drawdown_dev_max_g |
For every time moment, j=1,...J , portfolio -drawdown = -d(j) = maxn (-(uncompounded cumulative portfolio return at time moment n ) + (uncompounded cumulative portfolio return at time moment j )). Drawdown Maximum for Gain = Maximum Component Positive of vector (-d(1), ...,- d(J)) = largest component of the vector (-d(1), ..., -d(J)). |
|
entropyr |
Relative entropy where probabilities are variables. |
|
exp_eut |
Exponential Utility function for Linear Loss scenarios calculated with Matrix of Scenarios. |
|
fxchg |
Sum of fixed changes for absolute values of components of a vector exceeding some thresholds |
|
fxchg_neg |
Sum of fixed changes for components of -(vector) exceeding some thresholds |
|
fxchg_pos |
Sum of fixed changes for components of a vector exceeding some thresholds |
|
kb_err |
Koenker and Bassett error of Linear Loss scenarios calculated with Matrix of Scenarios. Used for estimation of Value-at-Risk (i.e., percentile) in Linear Regression. |
|
linear |
Linear function with many variables |
|
log_eut |
Log Utility function for Linear Loss scenarios calculated with Matrix of Scenarios. |
|
log_sum |
Linear combination of logarithms of components of a vector |
|
logexp_sum |
Likelihood function in Logistic Regression |
|
max_comp_abs |
L-infinity norm of a vector, i.e., the largest absolute value of components of the vector |
|
max_comp_neg |
Maximal (largest) component of -(vector) |
|
max_comp_pos |
Maximal (largest) component of a vector |
|
max_dev |
Maximum of ((Linear Loss ) - (Average over Linear Loss scenarios)) scenarios. |
|
max_dev_g |
Maximum of (-(Linear Loss ) + (Average over Linear Loss scenarios)) scenarios.. |
|
max_risk |
Maximum of Linear Loss scenarios. |
|
max_risk_g |
Maximum of -(Linear Loss ) scenarios. |
|
meanabs_dev |
Mean Absolute Deviation for Linear Loss scenarios. |
|
meanabs_pen |
Mean Absolute for Linear Loss scenarios function. Calculated by averaging over scenarios the absolute values of losses . |
|
meanabs_risk |
Mean Absolute for Linear Loss scenarios. (Mean Absolute) =Average Loss + Mean Absolute Deviation. |
|
meanabs_risk_g |
Mean Absolute for Gain for Linear Loss scenarios. (Mean Absolute for Gain) = -Average Loss + Mean Absolute Deviation. |
|
meansquare |
Mean Square of Linear Loss scenarios calculated with Matrix of Scenarios or Expected Matrix of Products. |
|
pm_dev |
Expected access of ( (Loss ) - (Average Loss )) over some fixed threshold. |
|
pm_dev_g |
Expected access of (- (Loss ) + (Average Loss )) over some fixed threshold. |
|
pm_pen |
Expected access of ( (Loss ) - (Average Loss )) over some fixed threshold. |
|
pm_pen_g |
Expected access of -( Loss ) over some fixed threshold. |
|
pm2_dev |
Expected squared access of ((Loss ) - (Average Loss )) over some fixed threshold.
|
|
pm2_dev_g |
Expected squared access of (-(Loss ) + (Average Loss )) over some fixed threshold. |
|
pm2_pen |
Expected squared Linear Loss in access of of some fixed threshold. |
|
pm2_pen_g |
Expected squared Linear -(Loss ) in access of of some fixed threshold. |
|
pm2_pen_nd |
Expected squared Linear Loss in access of of some fixed threshold for the Loss with mutually dependent normally distributed random coefficients. |
|
pm2_pen_nd_g |
Expected squared Linear -(Loss ) in access of of some fixed threshold for the Loss with mutually dependent normally distributed random coefficients. |
|
pm2_pen_ni |
Expected squared Linear Loss in access of of some fixed threshold for Loss with independent normally distributed random coefficients. |
|
pm2_pen_ni_g |
Expected squared Linear -(Loss) in access of of some fixed threshold for Loss with independent normally distributed random coefficients. |
|
polynom_abs |
Sum of absolute values of components of a vector, i.e., L1 norm of a vector. |
|
pow_eut |
Power Utility function for Linear Loss scenarios calculated with Matrix of Scenarios. |
|
pr_dev |
Probability that (Loss)-(Average Loss) exceeds some fixed threshold. |
|
pr_dev_g |
Probability that -(Loss)+(Average Loss) exceeds some fixed threshold. |
|
pr_pen |
Probability that Linear Loss exceeds some fixed threshold. |
|
pr_pen_g |
Probability that Linear -(Loss ) exceeds some fixed threshold. |
|
quadratic |
Quadratic function |
|
st_dev |
Standard Deviation of Linear Loss scenarios calculated with Matrix of Scenarios. |
|
st_pen |
Root Squared Error of Linear Loss scenarios calculated with Matrix of Scenarios or Expected Matrix of Products. By definition, it is an average of squared loss scenarios. |
|
st_risk |
(Standard Deviation of Linear Loss scenarios)+(Average of Linear Loss scenarios). It is calculated with Matrix of Scenarios. |
|
st_risk_g |
(Standard Deviation of Linear Loss scenarios)-(Average of Linear Loss scenarios). It is calculated with Matrix of Scenarios. |
|
var_comp_neg |
α*I -th value in the ordered ascending sequence of components of a -(I-dimensional vector), where 0≤α≤1; e.g., α=0.8, I=100, we order components of the -(vector) and take the element number α*I = 80 |
|
var_comp_pos |
Maximal (largest) component of a vector . |
|
var_dev |
Value-at-Risk for (Linear Loss ) - (Average over Linear Loss scenarios) , i.e., α% percentile of (Linear Loss) - (Average over Linear Loss scenarios) scenarios. |
|
var_dev_g |
Value-at-Risk for -(Linear Loss ) + (Average over Linear Loss scenarios) , i.e., α% percentile of -(Linear Loss) + (Average over Linear Loss scenarios) scenarios. |
|
var_risk |
Value-at-Risk for Linear Loss scenarios, i.e., α% percentile of Linear Loss scenarios. |
|
var_risk_g |
Value-at-Risk for -(Linear Loss ) scenarios, i.e., α% percentile of -(Linear Loss) scenarios. |
|
variance |
Variance of Linear Loss scenarios calculated with Matrix of Scenarios. |
