<< Click here to display Table of Contents >> Navigation: Main Objects of PSG > Functions > Scenario Functions:

Recourse

Contents

Recourse function is a random convex function used for formulating, solving, and analyzing Two-Stage linear stochastic optimization problems.

Recourse Function is an analogue of the linear Scenario Loss and Gain Functions. Random coefficients in the Two-Stage stochastic problem have a finite joint discrete distribution (finite set of scenarios). Recourse Function provides an optimal value of the second stage linear optimization problem for every scenario of random coefficients of the Two-Stage problem.

Recourse Function is used as an argument of a Risk Function. Recourse Function can be used outside of Risk Function only for calculation of its scenario values.

Syntax

Mathematical Definition

Intput Arguments

Examples of Risk Functions on Recourse

Examples of Optimization Problem with Recourse

Examples of Calculation Problem with Recourse

List of PSG Functions for Recourse

See also

Syntax

risk_function(recourse(matrix_xfirst, matrix_subproblem, matrix_of_scenarios))	Recourse Function as an argument of Risk Function (short form).
risk_function_name1(recourse_name2(matrix_xfirst, matrix_subproblem, matrix_of_scenarios))	Recourse Function as an argument of Risk Function (with optional names).
recourse(matrix_xfirst, matrix_subproblem, matrix_of_scenarios)	Calculation values of Recourse Function for all scenarios.

Mathematical Definition

Let

be the first stage decision vector in a Two-Stage stochastic programming problem;

be the second stage decision vector in a Two-Stage stochastic programming problem;

be a scenario number of the Recourse Function;

be a probability of scenario , where .

Recourse function calculates discrete values (scenarios) of the linear optimization problem.

A scenario of recourse function, for a given value of decision vector , is calculated as follows

where

= vector of coefficients corresponding to the first stage decision vector ;

= vector of coefficients corresponding to the second stage decision vector ;

= optimal solution of the following second stage problem:

(1)

subject to

linear constraints for the second stage

(2)

bounds on the second stage decision variables

(3)

where

= matrices for the second stage linear constraints;

= vectors of lower and upper bounds for the second stage linear constraints;

= lower and upper bounds for the second stage variables, .

Note. Problem (1)-(3) is deterministic and is convex piece-wise linear function of the decision vector .

Intput Arguments

matrix_xfirst is a PSG matrix in the following format:

where the header row contains names of the first stage decision variables. Numerical data in this matrix (zeros) are not used.

matrix_subproblem is a PSG matrix providing information on one instance of the second stage problem. This matrix gives the names of the second stage variables and fixed numerical values for all elements of the second stage problem. However, only elements of the matrix defining deterministic components of the second stage problem are used. Stochastic elements of the second stage problem (depending on scenarios) are redefined in the matrix matrix_of_scenarios.

matrix_subproblem has the following format:

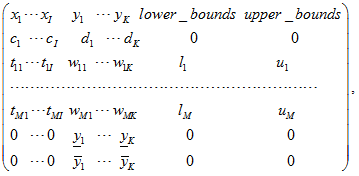
where the header row contains names of variables. Other rows contain numerical data.

Columns with names contain data for vector and matrix .

Columns with names contain data for vector , matrix and bounds .

Columns with names lower_bounds and upper_bounds contain bound vectors for constraints (2).

If some of bounds or are not used in the second stage problems, then corresponding values should be equal to –1E20 or +1E20 (which are considered by solver as “–infinity” and “+infinity”).

matrix_of_scenarios contains scenarios of random elements of the second stage problem in the following format:

Every element of the header row points out to a random element of the second stage problem. The other rows of this matrix contain numerical data. Element of the header row contains a column name, , and a row number, in brackets, for a random element of the matrix "matrix_subproblem". denotes the total number of random elements in the matrix "matrix_subproblem". is the -th scenario of the -th random element in the matrix "matrix_subproblem", ; .

The scenario_probability column contains probabilities of scenarios of random elements. This column is optional. If this column is not present in the matrix, then all scenarios have equal probability .

Examples of Risk Functions defined on Recourse Function

Risk functions defined on Recourse function

avg(recourse(matrix_xfirst, matrix_subproblem, matrix_of_scenarios) )

cvar_risk_g(0.9, recourse(matrix_xfirst, matrix_subproblem, matrix_of_scenarios) )

pr_dev(80, recourse(matrix_xfirst, matrix_subproblem, matrix_of_scenarios) )

st_pen( recourse(matrix_xfirst, matrix_subproblem, matrix_of_scenarios) )

Examples of Optimization Problem with Recourse

See Example of Optimization Problem.

Examples of Calculation Problem with Recourse

See Example of Calculation Problem.

List of PSG Functions for Recourse

Full Name	Brief Name	Short Description (in case of recourse function)
Average Loss	avg	Average of Recourse scenarios.
Average Gain	avg_g	Average of –Recourse scenarios.
CVaR Deviation	cvar_dev	Conditional Value-at-Risk for (Recourse –(Average Recourse)) scenarios, i.e., the average of largest (1-α)% of (Recourse - Average Recourse) scenarios.
CVaR Deviation for Gain	cvar_dev_g	Conditional Value-at-Risk for –(Recourse –(Average Recourse)) , i.e., the average of largest (1-α)% of –(Recourse – Average Recourse) scenarios.
CVaR	cvar_risk	Conditional Value-at-Risk (also called Expected Shortfall and Tail VaR) for Recourse scenarios, i.e., the average of largest (1-α)% of Recourse scenarios.
CVaR for Gain	cvar_risk_g	Conditional Value-at-Risk (also called Expected Shortfall and Tail VaR) for –Recourse scenarios, i.e., the average of largest (1-α)% of –Recourse scenarios.
Maximum Deviation	max_dev	Maximum of (Recourse –(Average Recourse)) scenarios.
Maximum Deviation for Gain	max_dev_g	Maximum of –(Recourse –(Average Recourse)) scenarios..
Maximum	max_risk	Maximum of Recourse scenarios.
Maximum for Gain	max_risk_g	Maximum of –Recourse scenarios.
Mean Absolute Deviation	meanabs_dev	Mean Absolute Deviation for Recourse scenarios.
Mean Absolute Error	meanabs_pen	Mean Absolute for Recourse scenarios. Calculated by averaging the absolute values of Recourse scenarios.
Mean Absolute Risk	meanabs_risk	Mean Absolute Risk for Recourse scenarios. (Mean Absolute Risk) = (Mean Absolute Deviation for Recourse)+ (Average Recourse).
Mean Absolute Risk for Gain	meanabs_risk_g	Mean Absolute Risk Gain for Recourse scenarios. (Mean Absolute Gain Risk) = (Mean Absolute Deviation for Recourse)–(Average Recourse).
Mean Square Error	meansquare	Mean Square Error of Recourse scenarios.
Partial Moment Deviation	pm_dev	Expected access of (Recourse –(Average Recourse)) over some fixed threshold.
Partial Moment Gain Deviation	pm_dev_g	Expected access of –(Recourse –(Average Recourse)) over some fixed threshold.
Partial Moment Deviation	pm_pen	Expected access of Recourse over some fixed threshold.
Partial Moment for Gain	pm_pen_g	Expected access of –Recourse over some fixed threshold.
Partial Moment Two Deviation for Loss	pm2_dev	Expected squared access of (Recourse –(Average Recourse)) over some fixed threshold.
Partial Moment Two Deviation for Gain	pm2_dev_g	Expected squared access of –(Recourse –(Average Recourse)) over some fixed threshold.
Partial Moment Two	pm2_pen	Expected squared Recourse in access of some fixed threshold.
Partial Moment Twofor Gain	pm2_pen_g	Expected squared –Recourse in access of some fixed threshold.
Probability of Exceedance Deviation	pr_dev	Probability that (Recourse –(Average Recourse)) exceeds some fixed threshold.
Probability of Exceedance Deviation for Gain	pr_dev_g	Probability that –(Recourse –(Average Recourse)) exceeds some fixed threshold.
Probability of Exceedance	pr_pen	Probability that Recourse exceeds some fixed threshold.
Probability of Exceedance for Gain	pr_pen_g	Probability that –Recourse exceeds some fixed threshold.
Standard Deviation	st_dev	Standard Deviation of Recourse scenarios.
Root Mean Squared Error	st_pen	Root Mean Squared Error of Recourse scenarios.
Standard Risk	st_risk	(Standard Deviation of Recourse) + (Average of Recourse)
Standard Gain	st_risk_g	(Standard Deviation of Recourse) – (Average of Recourse)
VaR Deviation	var_dev	Value-at-Risk for (Recourse – (Average Recourse)), i.e., α% quantile of (Recourse – (Average Recourse)) scenarios.
VaR Deviation for Gain	var_dev_g	Value-at-Risk for –(Recourse) + (Average Recourse) , i.e., α% quantile of –(Recourse) + (Average Recourse) scenarios.
VaR	var_risk	Value-at-Risk for Recourse scenarios, i.e., α% quantile of Recourse scenarios.
VaR for Gain	var_risk_g	Value-at-Risk for –Recourse scenarios, i.e., α% quantile of –Recourse scenarios.
Variance	variance	Variance of Recourse scenarios.