Root Mean Squared Error Normal Dependent (st_nd_err)
Root Mean Squared Error Normal Dependent. Squared Error of Linear Loss with mutually dependent normally distributed random coefficients. It is calculated with Matrix of Means (one row matrix) and Covariance Symmetric Matrix.
Syntax
st_nd_err(matrix_mn,matrix_cov) |
short call; |
st_nd_err_name(matrix_mn,matrix_cov) |
call with optional name. |
Parameters
matrix_mn is a PSG matrix of mean values:

where the header row contains names of variables. The second row contains numerical data.
matrix_cov is a PSG matrix of covariance values:
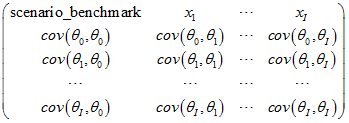
where the header row contains names of variables. Other rows contain numerical data.
Output
When function Root Mean Squared Error Normal Dependent is used in optimization or calculation problems PSG automatically calculates and includes in the solution report two outputs:
pseudo_R2_function_name |
|
contributions(function_name) |
Mathematical Definition
Root Mean Squared Error Normal Dependent function is calculated as follows:
![]() ,
,
where
![]() ,
,
![]() ,
,
![]() is an argument of function.
is an argument of function.
Remarks
Matrix matrix_cov have to be symmetric.
Example
See also
Mean Absolute Error, Mean Absolute Error Normal Independent, Mean Absolute Error Normal Dependent, Mean Square Error, Mean Square Error Normal Independent , Mean Square Error Normal Dependent, Root Mean Squared Error, Root Mean Squared Error Normal Independent, Koenker and Basset Error, Rockafellar Error
