Probability of Exceedance Deviation Multiple Normal Independent (prmulti_ni_dev)
Contents
Probability of Exceedance Deviation Multiple Normal Independent. There are M Linear Loss functions with independent normally distributed random coefficients.
Probability of Exceedance Deviation Multiple Normal Independent = 1-(Probability that all M Loss Deviation functions are below the threshold).
Syntax
prmulti_ni_dev(w, matrix_mn, matrix_vr) |
short call; |
prmulti_ni_dev_name(w, matrix_mn, matrix_vr) |
call with optional name. |
Parameters
is a threshold.
matrix_mn is a PSG matrix of mean values of coefficients of Loss functions:
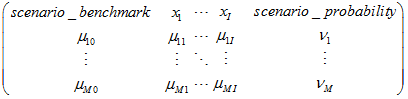
where the header row contains names of variables. Other rows contain numerical data.
matrix_vr is a PSG matrix of variance values of coefficients of Loss functions:
where the header row contains names of variables. Other rows contain numerical data.
Mathematical Definition
The Probability of Exceedance Deviation Multiple Normal Independent is calculated as follows:
where
,
is standard Deviation of Loss Functions;
are random functions;
is a 
-th Loss function;
is an argument of function.
Example
See also