Solution in MATLAB Environment
Table 1. Solutions of Problem with CDaR_DEV Multiple and Problem with CDaR_DEV Single
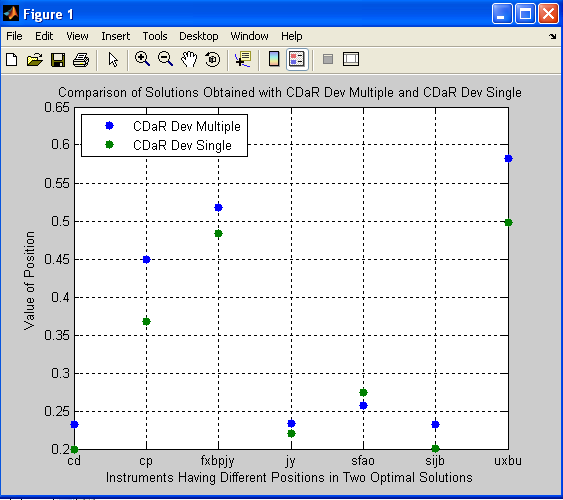
Figure 1. Comparison of Solutions Obtained with CDaR Dev Multiple and CDaR Dev Single
Two optimization problems: maximization of average annualized portfolio return with constraints on CDaR Deviation Multiple ( for multiple paths) and maximization of average annualized portfolio return with constraints on CDaR Deviation (for united single path). For more details about these problems see Formal Problem Statement or:
MATLAB code for Portfolio Optimization with Drawdown Constraints, Single Path vs Multiple Paths is in file CS_CDaR_Single_Path_vs_CDaR_Multiple_Paths_Toolbox.m.
Data are saved in file CS_CDaR_Single_Path_vs_CDaR_Multiple_Paths_Toolbox_data.mat.
Let us describe the main operations. To run case study you need to do the following main steps:
In file CS_CDaR_Single_Path_vs_CDaR_Multiple_Paths_Toolbox.m:
Load data prepared in PSG Toolbox format and packed in structure 'toolboxstruc_arr':
load CS_CDaR_Single_Path_vs_CDaR_Multiple_Paths_Toolbox_data.mat 'toolboxstruc_arr'
tbpsg_export_to_workspace(toolboxstruc_arr);
Generate problem statement for CDaR Deviation Multiple:
str1_1 = sprintf('maximize');
str1_2 = sprintf('linear_average_returns(matrix_average_annualized_returns)');
str1_3 = sprintf('Constraint: <= 0.023');
str1_4 = sprintf('cdarmulti_dev(0.8, matrix_1,...,matrix_11)');
str1_5 = sprintf('Box: >= point_lowerbounds, <= point_upperbounds');
str1_6 = sprintf('Solver: TANK, precision = 9');
clear problem_statement1;
problem_statement1 = sprintf('%s\n', str1_1, str1_2, str1_3, str1_4, str1_5, str1_6);
% Uncomment the following line to open the problem in Toolbox Window
% tbpsg_toolbox(problem_statement,toolboxstruc_arr);
Optimize the first problem:
[solution_str1, outargstruc_arr1] = tbpsg_run(problem_statement1, toolboxstruc_arr);
Extract optimal solution:
point_variables1 = tbpsg_optimal_point_vars(solution_str1, outargstruc_arr1);
Points1 = tbpsg_optimal_point_data(solution_str1, outargstruc_arr1)';
Generate problem statement for CDaR Deviation Single:
str2_1 = sprintf('maximize');
str2_2 = sprintf('linear(matrix_average_annualized_returns)');
str2_3 = sprintf('Constraint: <= 0.023');
str2_4 = sprintf('cdar_dev(0.8, matrix_H)');
str2_5 = sprintf('Box: >= point_lowerbounds, <= point_upperbounds');
str2_6 = sprintf('Solver: TANK, precision = 9');
clear problem_statement2;
problem_statement2 = sprintf('%s\n', str2_1, str2_2, str2_3, str2_4, str2_5, str2_6);
% Uncomment the following line to open the problem in Toolbox Window
% tbpsg_toolbox(problem_statement,toolboxstruc_arr);
Optimize the second problem:
[solution_str2, outargstruc_arr2] = tbpsg_run(problem_statement2, toolboxstruc_arr);
Extract optimal solution:
point_variables2 = tbpsg_optimal_point_vars(solution_str2, outargstruc_arr2);
Points2 = tbpsg_optimal_point_data(solution_str2, outargstruc_arr2)';
Table 1. Solutions of Problem with CDaR_DEV Multiple and Problem with CDaR_DEV Single
Solution with CDaR_DEV Multiple Solution with CDaR_DEV Single
Objective: 0.2408 0.2289
Components:
ad 0.2000 0.2000
bd 0.2000 0.2000
bp 0.2000 0.2000
cd 0.2319 0.2000
cp 0.4495 0.3681
dx 0.2000 0.2000
ed 0.2000 0.2000
eu 0.2000 0.2000
fxadjy 0.2000 0.2000
fxbpjy 0.5181 0.4836
fxeubp 0.2000 0.2000
fxeujy 0.2000 0.2000
fxnzus 0.2000 0.2000
fxussg 0.2000 0.2000
fxussk 0.2000 0.2000
fy 0.2000 0.2000
gc 0.2000 0.2000
jy 0.2333 0.2209
lift 0.2000 0.2000
ligi 0.2000 0.2000
liib 0.2000 0.2000
lmal 0.2000 0.2000
manb 0.2000 0.2000
sf 0.2000 0.2000
sfao 0.2576 0.2743
sfbd 0.2000 0.2000
si 0.2000 0.2000
sijb 0.2319 0.2010
sini 0.2000 0.2000
ty 0.2000 0.2000
uxbu 0.5825 0.4977
Figure 1. Comparison of Solutions Obtained with CDaR Dev Multiple and CDaR Dev Single