VaR Deviation for Mixture of Normal Independent. Consider a mixture of (random) Linear Loss functions with positive weights summing up to one. Coefficients in all  Linear Loss functions are independent normally distributed random values. avg_var_ni_dev is the VaR of the mixture of Normally Independent random values.

 

Syntax

 
Parameters

matrix_mn        is a PSG matrix of mean values:

       

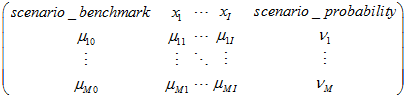
where the header row contains names of variables. Other rows contain numerical data.

 

matrix_vr        is a PSG matrix of variance values:

       

where the header row contains names of variables. Other rows contain numerical data.

       is a confidence level.

 

Mathematical Definition

VaR Deviation for Mixture of Normal Independent function with confidence level is calculated by minimizing of threshold under constraint on Average Probability of Exceedance Deviation for Loss Normal Independent:

.

is an argument of Average VaR Deviation Normal Independent function.

 

Example

 

See also

VaR Deviation for Gain for Mixture of Normal Independent,

VaR,

VaR Normal Independent, VaR  Normal Dependent,

VaR Deviation, VaR Deviation Normal Independent, VaR Deviation Normal Dependent,

VaR for Mixture of Normal Independent